2025.11.14ブログ
2025大学入学共通テスト 情報I 大問4の解説 : 旅行・観光消費動向調査のデータ分析 Part2

本日の記事はPart2ということで、問3と問4についても解説します。ここからは、更に一歩踏み込んだデータを読み解く力が試されます。一見すると複雑な「散布図」や「箱ひげ図」が登場しますが、心配いりません。これらの図も、読み取るためのコツさえつかめれば、出題者の意図が見えてきます。
それでは共通テストで実際に出題された問題を見て、データ分析の本質に迫っていきましょう!
共通テスト第4問での出題内容
問3
次の文章を読み、空欄[キ][ク]に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
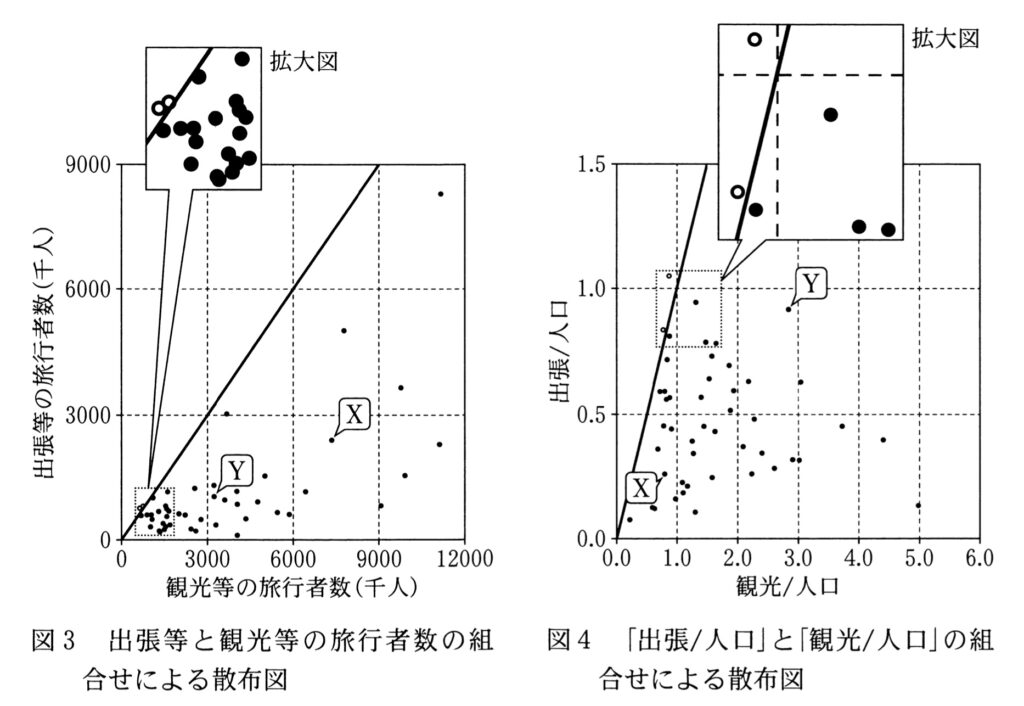
Uさんは、各都道府県の出張等と観光等の旅行者数の関係に着目し、縦軸と横軸の値が等しい直線を記入した散布図(図3)を作成した。この散布図中に完全に重なっている点はないが、多くの都道府県が観光等の旅行者数が3000千人以下の範囲に集中しているため、異なる指標を使った散布図も作成することにした。
Uさんは、人口が多い都道府県には旅行の目的地になる場所(企業や観光名所など)が多く、旅行先になりやすいのではないかと考え、「出張等と観光等の旅行者数を、旅行先の各都道府県の人口で割った値」を指標とし、それぞれを出張/人口,観光/人口と呼ぶことにした。これらの指標は、旅行先の人口を基準として相対的に各目的の旅行者が多いか少ないかの程度を示すことになる。そこでUさんは、総務省統計局が公開している2019年度の都道府県ごとの人口のデータ(表3)を入手し、「出張/人口」と「観光/人口」の組合せについて、縦軸と横軸の値が等しい直線を記入した散布図(図4)を作成した。なお、この散布図中に完全に重なっている点はない。
図3と図4のいずれの散布図にも、直線の上側に白抜きの丸で示した二つの点がある。各図の白抜きの二つの点について、[キ]。
また、これらの散布図上にある点Xと点Yは、それぞれ同じ都道府県を示している。二つの散布図でこれらの点について、縦軸と横軸の両方で値の大小が逆転している理由は、点Xの都道府県よりも点Yの都道府県の方が[ク]ためである。

[キ]の解答群
0 両方の図で同じ二つの都道府県を示している
1 一つは両方の図で同じ都道府県を示し、もう一つは異なる都道府県を示している
2 両方の図で異なる二つの都道府県を示している
3 これらの図からだけでは、同じ都道府県であるかはわからない
[ク] の解答群
0 出張等の旅行者数が多い
1 観光等の旅行者数と出張等の旅行者数の差が大きい
2 観光等の旅行者数を出張等の旅行者数で割った値が小さい
3 人口が少ない
問4
次の文章を読み、空欄[ケ]に当てはまる数字をマークせよ。また、空欄[コ]〜[シ]に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。
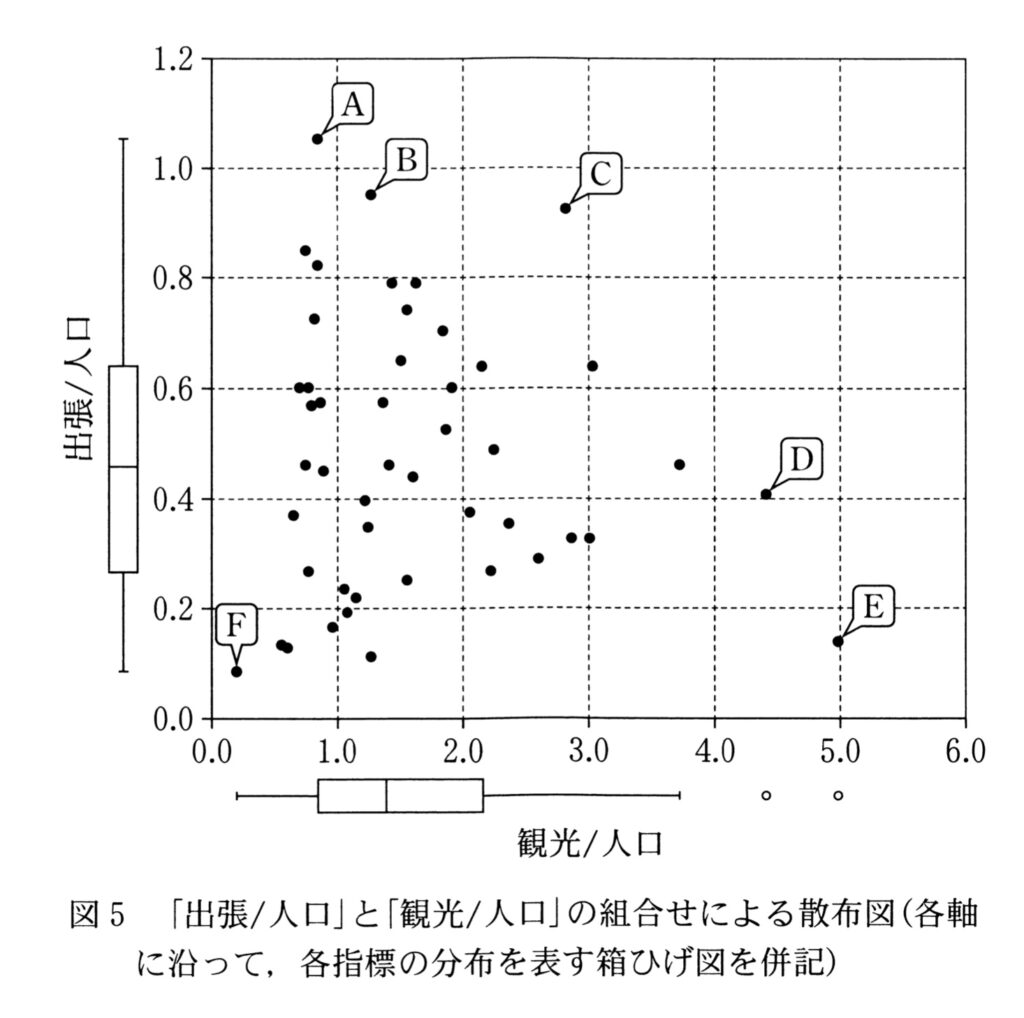
Uさんは、「出張/人口」と「観光/人口」の関係について、より詳しく分析することにした。そこで、図4の散布図の各軸に沿って各指標の分布を表す箱ひげ図(外れ値は。で表記)を併記したもの(図5)を作成した。
図5を見ると、例えば、観光等の旅行者が人口の4倍以上訪れる都道府県を表す点の数は[ケ]個である。このように、指標の値を見ることで、都道府県の人口に対して目的別の旅行者数がどの程度であったかを知ることができる。
そこでUさんは、今回の分析において、「出張/人口」がその第3四分位数より大きい都道府県を出張等が多めの都道府県、「観光/人口」がその第3四分位数より大きい都道府県を観光等が多めの都道府県と呼ぶことにした。このように決めた場合、[コ]が最も多い。
Uさんは、「出張等も観光等も多めの都道府県」と、「出張等は多めではないが観光等は多めの都道府県」がなぜそのような状況になっているのかに興味をもった。図5においてA~Fで示した都道府県のうち、「出張等も観光等も多めの都道府県」は[サ]である。一方、「出張等は多めではないが観光等は多めの都道府県」は複数あるが、その中で「出張/人口」を「観光/人口」で割った値が最も小さい都道府県を考えると、[シ]となる。
[コ] の解答群
0 出張等も観光等も多めの都道府県
1 出張等は多めではないが観光等は多めの都道府県
2 出張等は多めだが観光等は多めではない都道府県
3 出張等も観光等も多めではない都道府県
[サ][シ]の解答群
0 Aの都道府県
1 Bの都道府県
2 Cの都道府県
3 Dの都道府県
4 Eの都道府県
5 Fの都道府県
出典:独立行政法人 大学入試センター
そもそも「データを読み取る」とは?
問題の解説に入る前に、まずは私たち自身の「データを読み取る」ことに対する考え方を少し変えましょう。「データを読み取る」と聞くと、グラフの数字や点を単に追いかける作業だと感じてしまうかもしれません。でも本当のところは、そうでありません。データを読み取ることで、グラフの裏側に隠された意味や傾向、そしてデータ同士の意外な関係性を自分の手で見つけ出すことができます 。共通テストの出題者も、私たちがただ知識を覚えているかではなく、このデータの裏側にある真実を汲み取る力を試しているわけです。
私たちがデータから知りたい真実には、多くのパターンがあります。だからこそ、グラフにもたくさんの種類があります。そして目的に合わせて適切なグラフを選ぶことで、データは一瞬で鮮やかな物語を語り始めます。以下では代表的な7つのグラフを紹介しているので、一緒に見ていきましょう!
棒グラフ
目的: 各項目の「絶対的な量」や「大きさ」を比較するための、最も基本的なグラフです。「どのカテゴリーが最も多いか?」「AとBの間に決定的な差はあるか?」を知りたい時に、迷わず選びましょう。
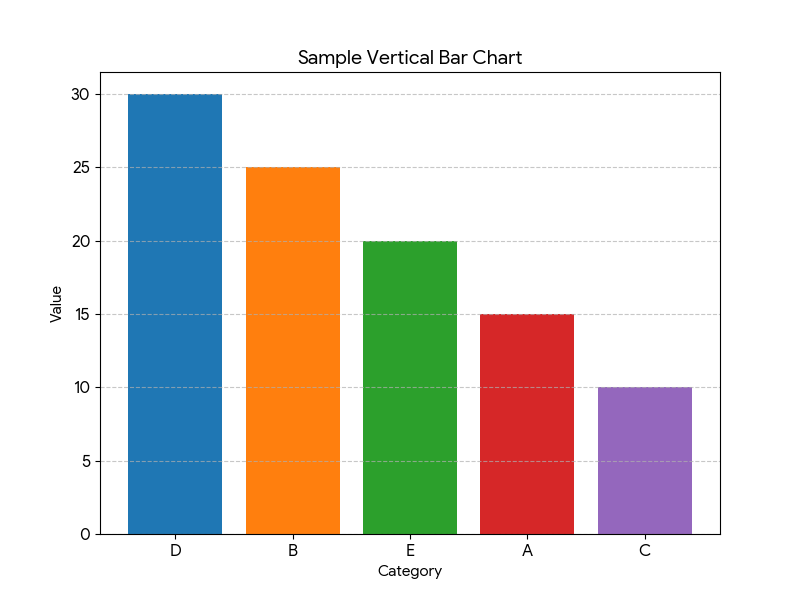
着眼点:
1. 棒の「高さ」を見る
これが棒グラフのすべてです。棒が高いほど、その量が多いことを示します。まず行うべきは、グラフ全体を見渡し、一番高い棒(最大値)と一番低い棒(最小値)を瞬時に見つけることです。これにより、全体の範囲と極端な値を把握できます。
2.棒同士の「差」を見る
Aの棒とBの棒の高さを比べ、差の大きさを把握します。AがBの「何倍くらいか」「差はどれくらいか」を見ることで、項目間の優劣や重要度が具体的にわかります。
3.棒の「並び順」を見る
もし棒が高さ順に並べられていれば、順位を示す意図が非常に強いです。また並び順がバラバラな場合は、時系列や地域など、別の要素に意味がある可能性があります。
円グラフ
目的: 全体を100%とした時に、それぞれの部分がどれくらいの割合を占めているかを知りたい時に使います。全体の構成比を把握して、「主要な要因は何か」「マイノリティの割合は」といった質問に答えるためのグラフです。
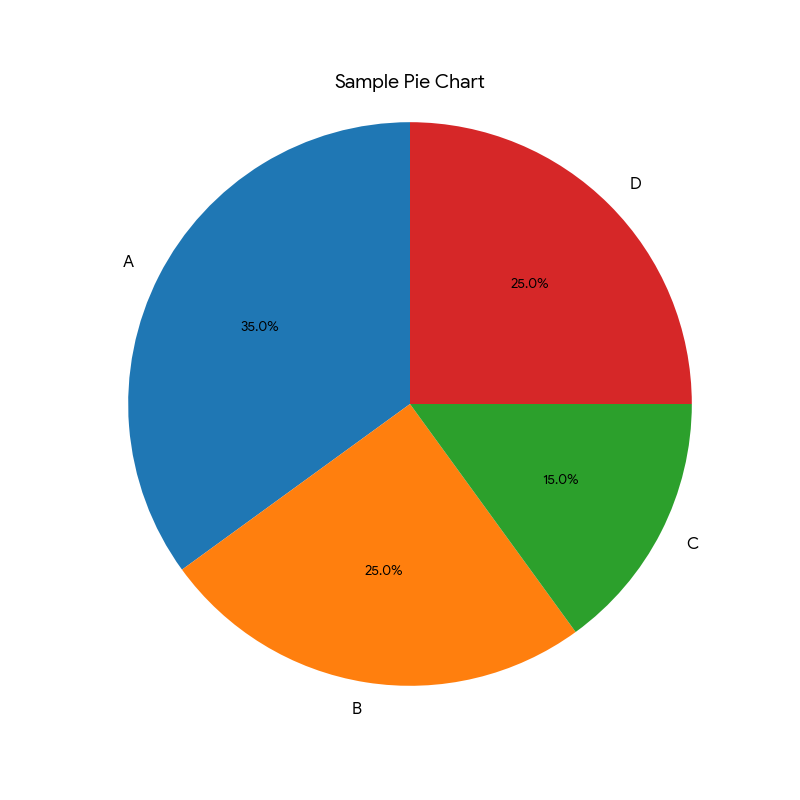
着眼点:
1.扇形の「面積」を見る
面積がそのまま、割合の大きさを示しています。まずは一番大きなパイは何か、そして一番小さなパイは何かを素早く見つけましょう。
2.基準線となる「50%」と「25%」と比較する
ある項目が「過半数を占めているか?」は、全体の傾向を決定づける最重要ポイントです。また25%のラインを意識することで、その項目が「4分の1の壁」を超えているかどうかが、すぐにわかります。
帯グラフ
目的: 全体に対する「内訳の割合」を見るという点では円グラフと同じですが、帯グラフは特に、複数のグループ(例:部署Aと部署B、年代別など)の間でその内訳の割合がどう異なっているかを比較する能力に非常に優れています。円グラフを並べるよりも、変化や違いが一目瞭然になります。
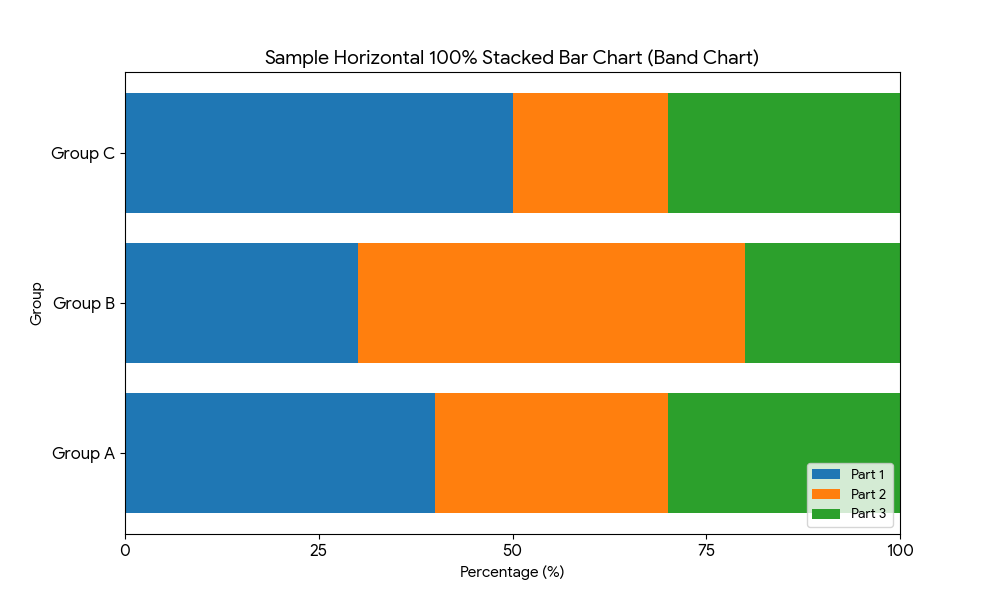
着眼点:
1.複数の帯を見比べる
これは帯グラフの最も重要な見方です。例えば、A組の帯とB組の帯を並べて、「賛成の部分の長さはどちらのグループで長いか?」を瞬時に比較します。
2.構成比の違いや変化を見る
例えば、「A組は男子の割合が多いが、B組は女子の割合が多い」といったグループ毎の明確な特徴を把握できます。またこれが時系列のデータであれば、「去年に比べて、今年は○○の割合が明らかに増えた」といったトレンドの変化も正確に捉えられます。
折れ線グラフ
目的: 時間の経過とともに、データがどのように「変化(推移)」したかを知りたい時に使います。「この売上は成長しているのか?」「気温はいつが最も過酷だったのか?」といった、トレンドや変遷を追跡するのに最適なグラフです。
着眼点:
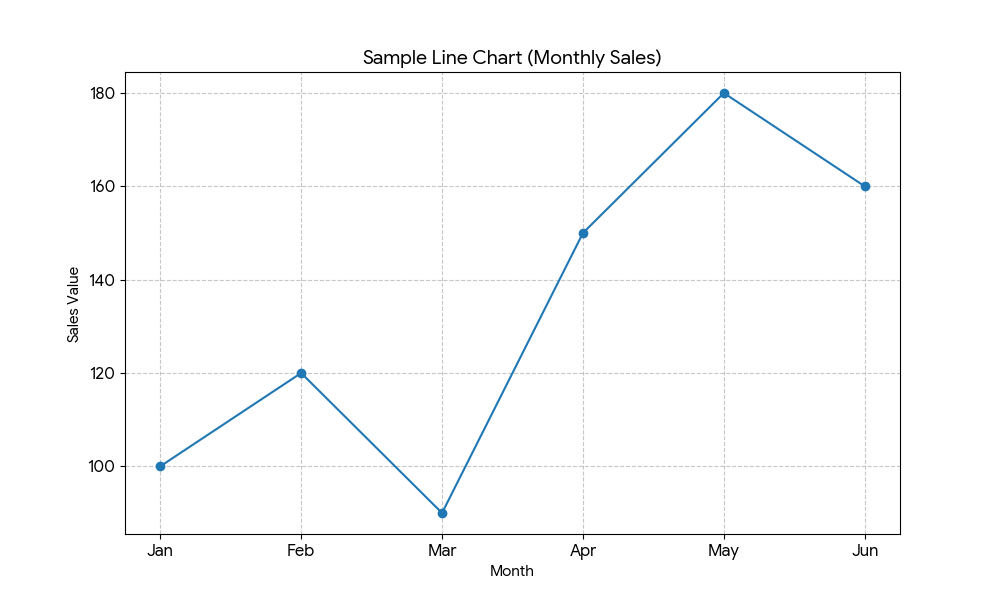
1.線の「傾き」を見る
グラフ全体を見て、「右肩上がり」か「右肩下がり」かを見ましょう。これにより、日々の小さな変動に惑わされず、長期的な増加傾向もしくは減少傾向かという、データが向かっている大局的なトレンドを把握できます。
2.「山」と「谷」を特定する
線が最も高くなっている山は最大値を示しており、最も低くなっている谷は最小値を示します。例えば売上のデータであれば、売上が一番良かった時、あるいは一番低かった時を明らかにしてくれます。
3.線の「交差」と「間隔」を見る
折れ線グラフの中に線が複数ある場合、線が交差する点は、2つのデータの順位が逆転したドラマチックなタイミングを示します。また2本の線の間隔が開いていくか、もしくは縮まっていくかを見ることで、両者の差が拡大しているのか、それとも競争が激しくなっているのかといった変動を読み取ることができます。
ヒストグラム
目的: データのちらばり具合(分布)を読み解くために使う、非常に強力なグラフです。データがどの範囲にどれだけの頻度で集中しているのかを把握し、「全体の傾向」や「集団の特性」を見抜きます。(例:テストの点数分布、身長の分布など)
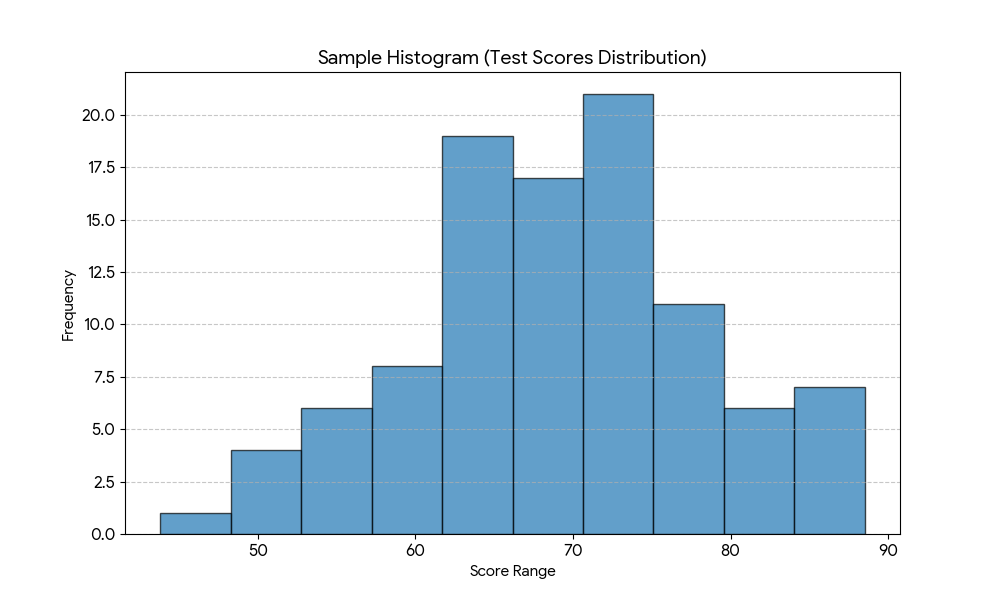
着眼点:
1.山の「形」を見る
対称な山(釣鐘型): データが平均値付近に最も多く集まっている、理想的できれいな分布です。(例:身長など、自然界に多い分布です)
右に裾が長い(左に偏った山): 多くのデータは小さい値に固まっていますが、ごく一部に非常に大きい値(お金持ち、高額所得者など)があります。(例:所得分布)
左に裾が長い(右に偏った山): 多くのデータは大きい値に集中していますが、ごく一部に非常に小さい値(苦手な人、未熟な人など)があります。(例:簡単なテストの点数分布)
2.山の「数」を数える
山が一つ: データが一つの均質な集団である可能性が高いです。
山が二つ以上: データの背景に、性質の異なる2つ以上のグループが混ざっている可能性があります。(例:テストの点数を男女でまとめて集計した場合、午前と午後の来客数を一緒に集計した場合など)
箱ひげ図
目的: ヒストグラムと同じくデータの「ちらばり具合(分布)」を見ますが、最大の特徴は、最小値、第1四分位数、中央値、第3四分位数、最大値というたった5つの数字で分布を非常にコンパクトに表現できることです。これにより、複数のグループの成績表を瞬時に並べて比較するのに最も強力なグラフとなります。
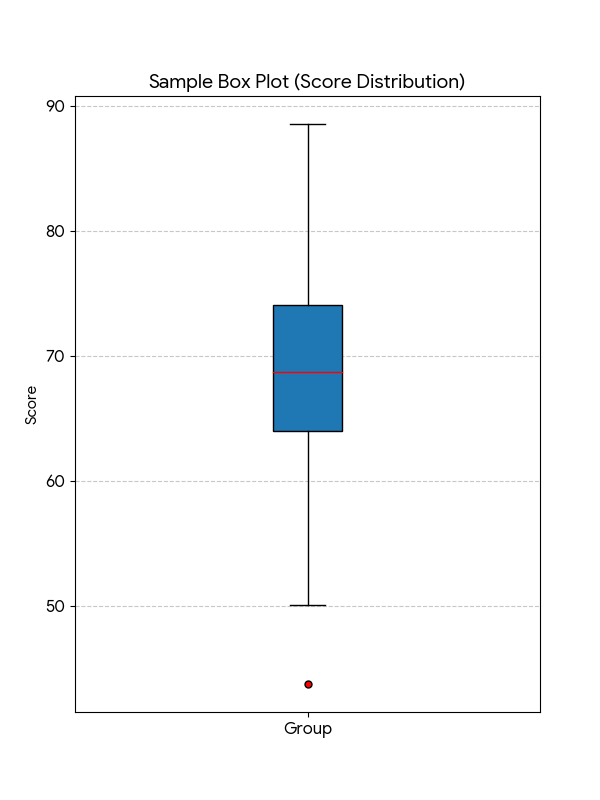
着眼点:
1箱の長さを見る
箱の長さは、データの中央50%がどの範囲にいるかを示します。箱が短いデータは、中央に集中しており、バラツキが小さい(平均的な層が密集している)ことを意味します。逆に箱が長い場合、データが広く散らばっている(上位層と下位層の幅が大きい)ことを意味します。
2.箱の中の線(中央値)を見る
この線は、データの「ど真ん中」の値です。この線が箱の真ん中より下側にあれば、データは「小さい値の側」に偏って集まっていることがわかります。また上側にあれば、「大きい値の側」に偏っている(左に裾が長い分布)ことがわかります。
3.「ひげ」の長さを見る
ひげは、中央50%から外れたデータがどれだけ広がっているかを示します。ひげが長いほど、最大値と最小値の差が大きい、つまりデータの幅が広いことを意味します。
4.箱の「位置」と「重なり」を見る
複数の箱ひげ図を比べる場合、Aの箱がBの箱より全体的に上にあれば、Aグループの方がBグループより全体的に値が大きい傾向があると読み取れます。箱同士の重なり具合を見ることで、両集団の共通点や違いが一目瞭然になります。
散布図
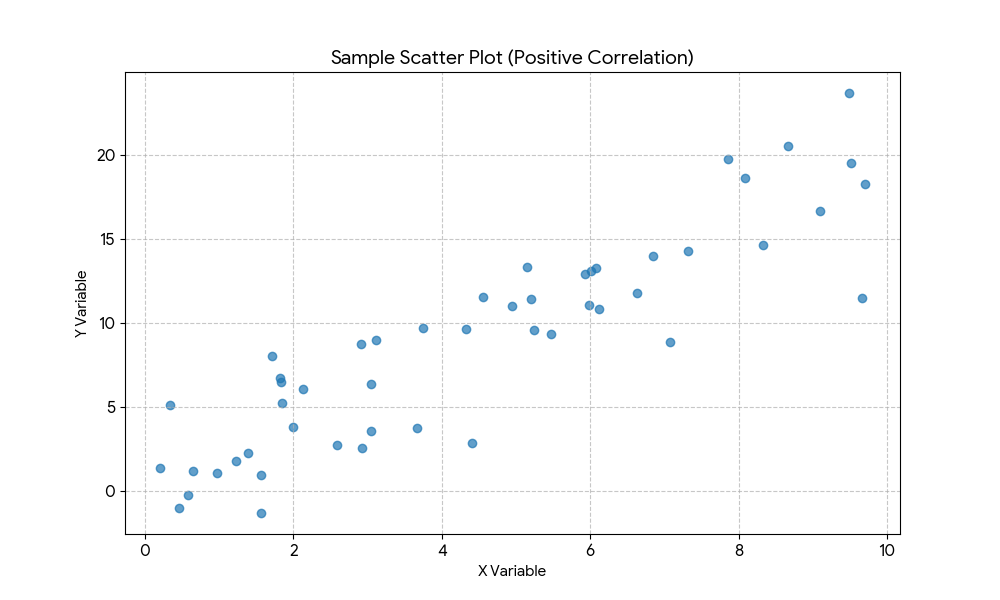
目的: 2つの異なるデータ(例:勉強時間と点数、気温とアイスの売上)の間に、どのような関係性があるかを視覚的に探りたいときに使用するグラフです。「Xが増えるとYは増えるのか、減るのか」といった、データ同士の連動性を知りたい時に使います。
着眼点:
1.点全体の「流れ」や「形」を見る
点が作るかたまりの向きが、データが持つ関係性を教えてくれます。例えばXが増えるとYも増える場合は右肩上がり になり、 「正の相関」があることを意味します。(例:身長と体重)逆にXが増えるとYは減る場合は右肩下がりとなり 「負の相関」になります。(例:気温と暖房費)またバラバラの場合は相関がないため、XとYに明確な関係は見られないことを意味します。
・点の「密集度」を見る
相関の強さは、点がどれだけ直線状に集まっているかで判断できます。例えば、点が直線的で、細く集まっているほど、「相関が強い」と言えます。つまり、2つのデータは非常に強い結びつきを持っているということです。逆に点が太く、ぼんやりと広がっているほど、「相関が弱い」と言えます。関係性はあるものの、例外やバラツキが大きいことを示唆します。
このように、データ分析の世界では、目的に応じてそれぞれ得意なグラフが存在します。そのため、私たちが「何を知りたいか」という目的を明確にすれば、どのグラフを使えばよいかが自然と決まります。そして各グラフの目的や着眼点を知っていることこそが、データが語る真実を正確に、また深く読み取るための第一歩となるのです。
直線の上下関係がポイント!
データ分析に対する心構えができたところで、いよいよ共通テストで出題された問題の解説に入ります。まずは[キ]の答えを考えるため、図3と図4の散布図に引かれた直線が持つ意味を理解しましょう。どちらの図にも、縦軸と横軸の値が等しい直線が引かれています。これは、2つのデータを比較するための基準線となっています。
- 図3:縦軸が「出張」、横軸が「観光」です。もし「出張 > 観光」なら、点は必ず直線の上側に来ます。
- 図4:縦軸が「出張/人口」、横軸が「観光/人口」です。もし「出張/人口 > 観光/人口」なら、点は必ず直線の上側に来ます。
出題者は、この問で私たちが比率の本質を理解しているかを試しています。そして、ここで大切なのが「出張 > 観光」という関係は、両辺を同じ正の数(人口)で割っても変わらないということです。つまり、図3で直線の上側にある点は、図4でも必ず直線の上側に来ます。
この問題では、白抜きの丸がどちらの図でも直線の上側にあることが示されています。したがって、これらは同じ都道府県を示している言えます。よって、[キ]の答えは選択肢0の「両方の図で同じ二つの都道府県を示している」となります。
なぜ逆転した?点Xと点Yの大小関係
次に、[ク]の答えを考えます。図3では「X > Y」だったのに、図4では「X < Y」と大小関係が逆転する理由を解き明かしましょう。まずは、2つの図で点Xと点Yが示すおおよその値を確認していきます。
図3:
・点X 観光=約7500, 出張=約2700
・点Y 観光=約3200, 出張=約1000
→この時点では、どちらも「X > Y」です。
図4:
・点X 観光=約0.8, 出張=約0.3
・点Y 観光=約3.0, 出張=約0.9
→なんと、どちらも 「X < Y」に逆転しています!
この逆転の理由は、問題文で「点Xの都道府県よりも点Yの都道府県の方が [ク] ためである」とされています。では早速、確認した上記の内容を踏まえてそれぞれの選択肢を見ていきましょう。
選択肢0:「出張等の旅行者数が多い」
先ほど確認した通り、出張の値は点Xで約2700、点Yで約1000と分かっているので、点Yの方が出張等の旅行者数は少ないです。そのため、この選択肢の内容は誤りです。
選択肢1:「観光等の旅行者数と出張等の旅行者数の差が大きい」
観光と出張の差を計算すると、点Xで約4800(=7500-2700)、点Yで約2200(=3200-1000)となり、点Yの方が差は小さいことがわかります。そのため、この選択肢の内容も誤りです。
選択肢2:「観光等の旅行者数を出張等の旅行者数で割った値が小さい」
これも計算をして求めると、点Xでは約2.7(=7500/2700)、点Yでは約3.2(=3200/1000)となります。そして点Yの方が、観光を出張で割った値が大きいことがわかるので、この選択肢の内容も誤りです。
選択肢3「人口が少ない」
図3の点Xを見ると、旅行者数の数は観光でも出張でも点Yより多いです。ただ図4の指標は「出張/人口」と「観光/人口」なので、人口の数が増えると人口1人あたりの指標に直した時に、値が小さくなります。そのため、この選択肢の内容は正しいです。
散布図の読み解き
次に、[ケ]の答えを考えましょう。ここでは、「観光等の旅行者が人口の4倍以上訪れる都道府県の数」が問われています。これは散布図の軸が示す本当の意味を正確に読み取れるかを出題者が私たちに試している、シンプルかつ重要な問題です。
先に述べた通り、散布図は2つの異なるデータの間に、どのような関係性があるかを視覚的に探りたいときに使用するグラフです。図5を確認すると、縦軸も横軸も単なる旅行者数ではなく、それぞれ「出張/人口」、「観光/人口」という指標になっています。ここで、横軸の指標は観光客の数がその都道府県の人口の何倍にあたるかを示しています。したがって、問われている人口の4倍以上という条件は、横軸の「観光/人口」が4.0以上の点を探せば良いということになります。
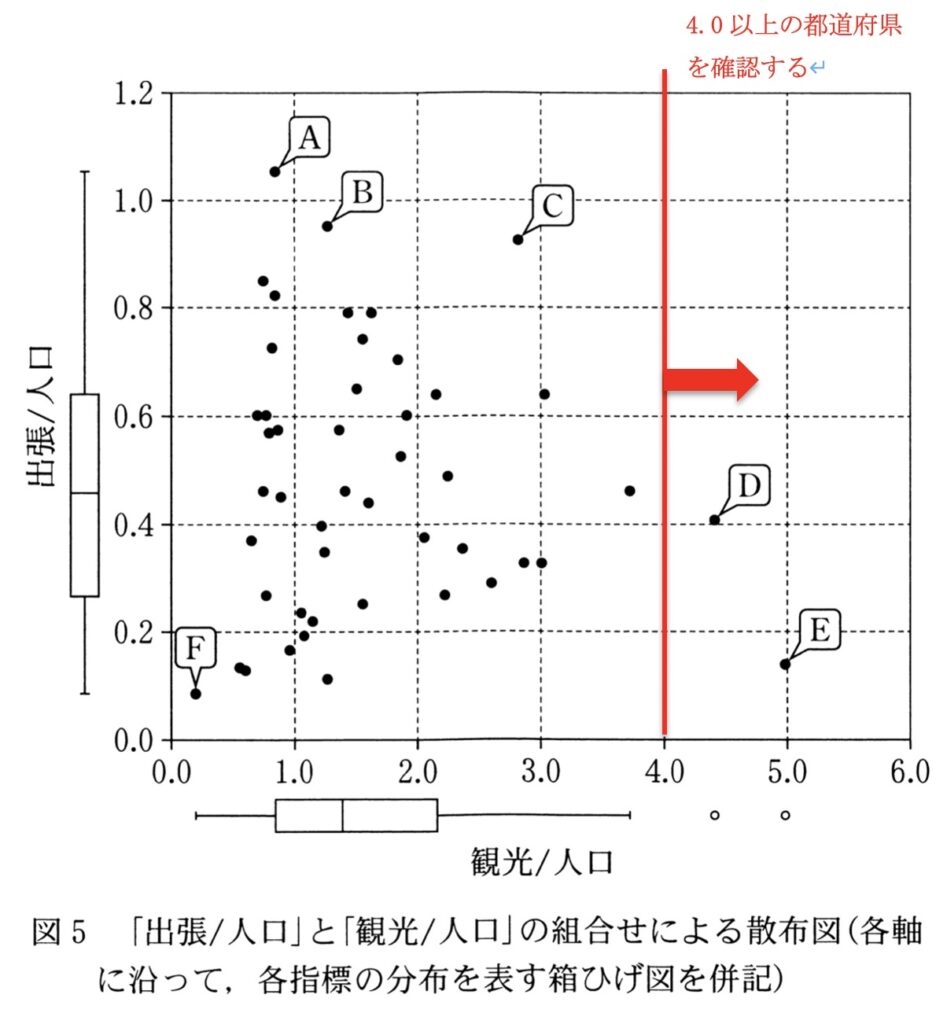
横軸の4.0よりも右側にある点は、明確に点Dと点Eの2つしかありません。そして点Dと点Eの2点が条件を満たしていることから、[ケ]の答えは2とわかります。このように軸の定義を正確に理解していれば、正しい回答を導き出すことができます。
箱ひげ図の理解がカギ!
いよいよ最後です。[コ]〜[シ]を解くためには、箱ひげ図を理解する必要があります。箱ひげ図は、データの分布を視覚的に示すグラフです。以下のように四角い箱と、上下に伸びる「ひげ」で構成されています。
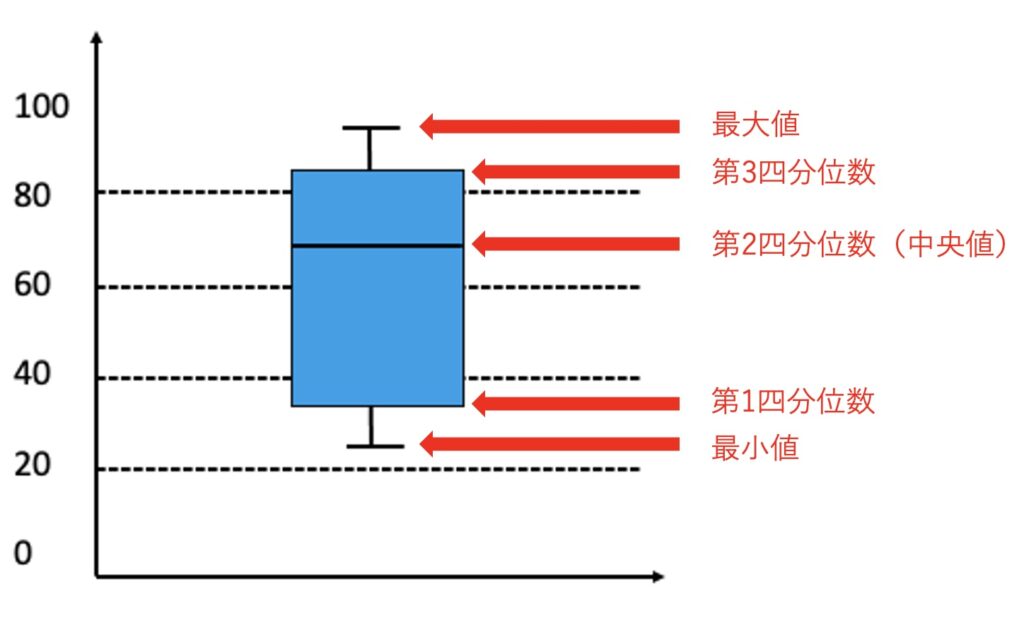
図の横にかかれている各用語の意味は、以下の通りです。
- 最大値: データの最も大きい値。上のひげの先端です。
- 第3四分位数: データを小さい順に並べた時、下から75%(4分の3)の位置にある値。箱の上側です。
- 中央値 / 第2四分位数: データを小さい順に並べた時、ちょうど真ん中(50%)の値。箱の中にある仕切り線です。
- 第1四分位数: データを小さい順に並べたとき、下から25%(4分の1)の位置にある値。箱の下側です。
- 最小値: データの最も小さい値。下のひげの先端です。
それでは、この知識を活用して[コ] の答えを考えていきましょう。問題文では、第3四分位数より大きい都道府県を「多め」と呼ぶルールが決められています。そこで出題者の定義に従って、図5の箱ひげ図の第3四分位数の位置から、下記のように境界線を引いてみましょう。
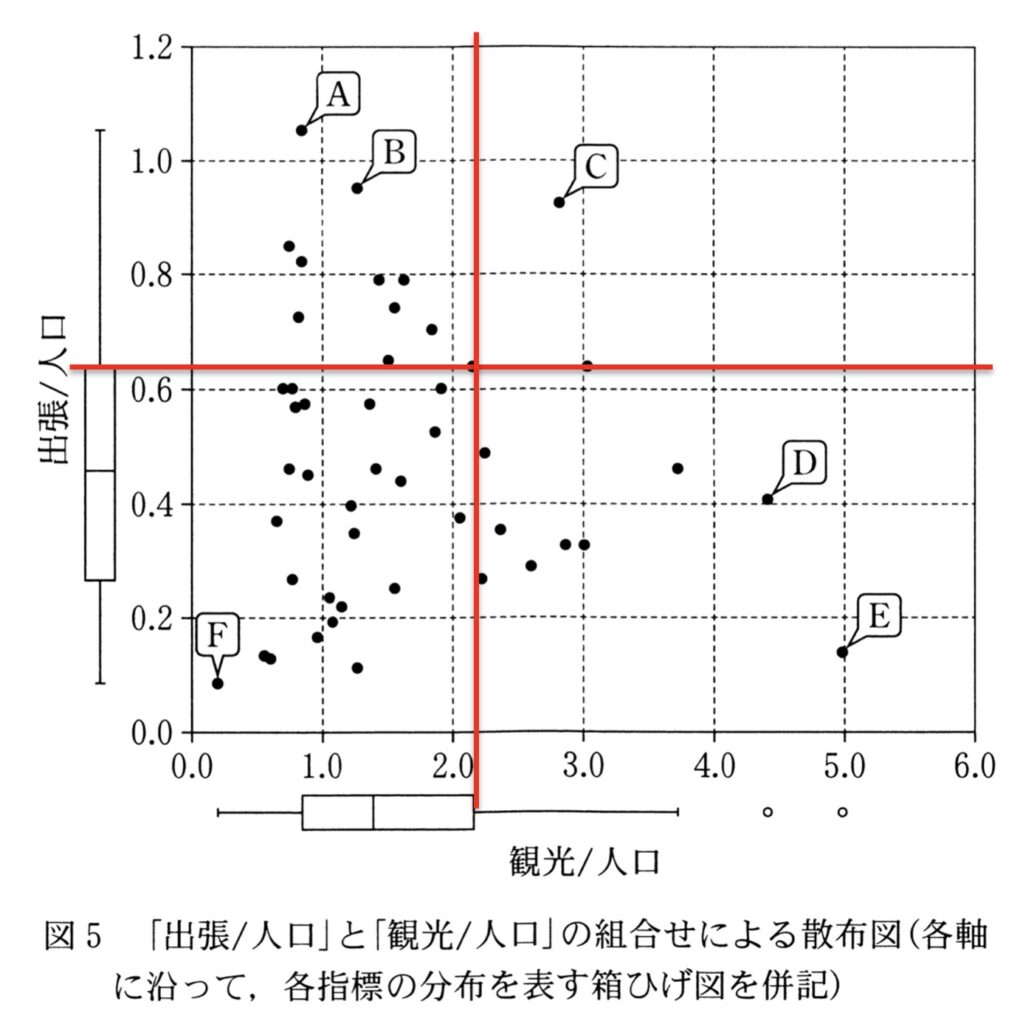
2本の境界線を引くと、上記のように散布図が4つの領域に分かれます。 この中で点の数が最も多い領域は、明らかに左下の領域です。そのため、[コ]の答えは選択肢3の「出張等も観光等も多めではない都道府県」となります。
次に、[サ] の答えを考えます。ここで問われているのは、「出張も観光も多め」、つまり右上の領域にある都道府県です。 A〜Fの中でこの領域に入っているのは点Cだけです。よって、[サ]の答えは選択肢2の「Cの都道府県」となります。
最後に、[シ] の答えを考えましょう。ここでは、「出張は多めではないが観光は多めの都道府県」が前提となっているので、右下の領域に注目します。そして「出張/人口」を「観光/人口」で割った値というのは、原点と各都道府県を示す点を結んだ直線の傾きと同じ意味なので、傾きが一番小さくなる点を見つければ良いことがわかります。図を見ると、点Eと原点を結んだ直線の傾きが最小になるので、[シ]の答えは選択肢4の「Eの都道府県」となります。
さいごに
ここまで読んで頂いた方には、単なる共通テスト対策を超えた「データ分析の面白さ」を、きっと感じて頂けたのではないでしょうか。一見すると複雑に思える問題も、散布図や箱ひげ図に関する基本的な知識を理解した上で読み解けば、そこに出題者の意図や社会のリアルな姿が浮かび上がってきます。この「データを正しく読み解く力」は、情報にあふれた現代社会を生き抜くための強力な武器になるはずです 。
今回の記事で、2025年共通テストの解説シリーズは最後となります。今までの記事で得た学びが、共通テスト本番だけでなく、これからの生活でも役立つことを心から願っています。本日も最後までお読み頂き、誠にありがとうございました。先月から始まった連載では、「AI時代を生き抜く」をテーマにした新しい内容をお届けしています。次回の記事も、ぜひ楽しみにお待ち下さい!
タイムレスエデュケーションは、東京都文京区小石川、本駒込、新宿区下落合にて、プログラミング&ロボット教室を開校しております。当教室はお子さまが「誰にも奪われない強み」を見つけ、自分の意思で未来を選べるようになるための教室です。毎回の授業で「探究→創造→発信」を繰り返す構造化カリキュラムを通じて、「論理的思考力」「集中力」「表現力・創造力」「問題解決力」を育みます。秋の無料体験会も開催致しますので、ご興味のある方はぜひお申し込みください。心よりお待ちしております。
コースについて

