2025.09.26ブログ
2025大学入学共通テスト 情報I 大問4の解説 : 旅行・観光消費動向調査のデータ分析 Part1
7月に公開した記事では、2025年の大学入学共通テスト「情報Ⅰ」で出題された内容のうち、ユーザインタフェースに関する問題について解説しました。本日の記事では、第4問の問1と問2で題材になっていた旅行・観光消費の動向調査について解説していきます。それでは早速、共通テストで実際に出題された問題の内容を見ていきましょう!
共通テスト第4問での出題内容
旅行が好きなUさんは、観光庁が公開している旅行・観光消費動向調査のデータのうち、2019年の結果を用いて、さまざまな観点で旅行に関する実態を分析してみることにした。なお、以下では延べ旅行者数を旅行者数と呼ぶ。
表1には、地方ごとに、その地方を主な目的地として宿泊旅行をした旅行者数がまとめられている。また、この表では、旅行の目的を出張等、帰省等、観光等の三つに分け、それぞれの旅行者数とその合計が集計されている。
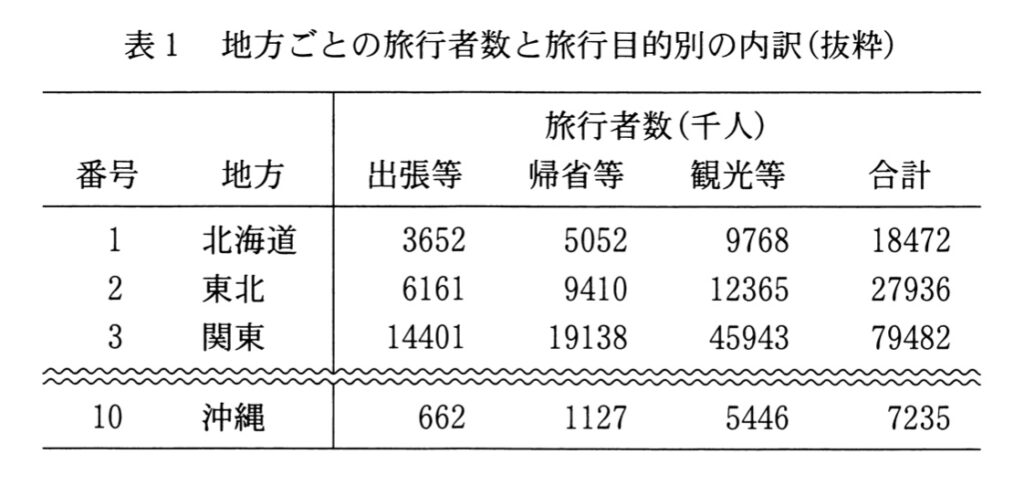
問1
次の文章を読み、空欄[ア] ~ [エ] に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、空欄 [ウ][ エ]の順序は問わない。
Uさんは、表1を見せながら、T先生に相談した。
Uさん:この表からわかる情報を把握しやすくするために、グラフを作ろうと思っています。
T先生:グラフを作る前に、表の各項目の尺度水準を確認してみましょう。地方については、どの尺度水準だと思いますか。
Uさん: 郵便番号などと同じで、[ア]だと思います。
T先生:そうですね。では、番号と地方以外の項目については、どうでしょうか。
Uさん: これらの項目は旅行者数を示すので、[イ] でしょうか。
T先生:はい、そのとおりです。それでは、地方による旅行者数の違いがわかりやすくなるように、棒グラフと帯グラフを作ってみましょう。
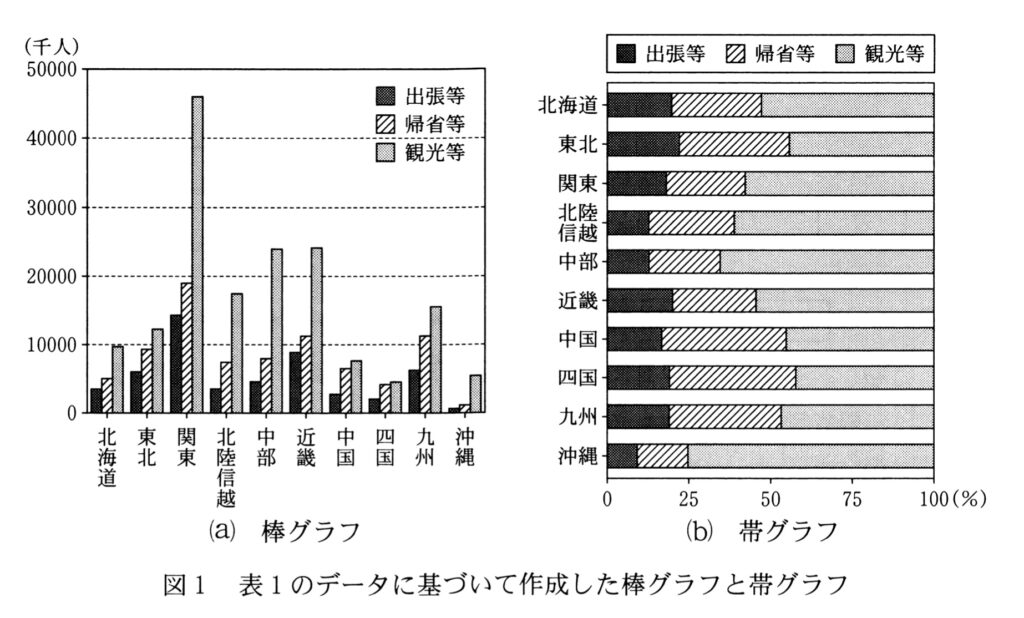
Uさんは、図1のグラフを作成した。これらのグラフから、 [ウ] ことや [エ] ことなど、地方による傾向の違いを読み取ることができた。
[ア] [イ] の解答群
0 比例尺度
1 間隔尺度
2 順序尺度
3 名義尺度
[ウ][エ]の解答群
0 帰省等を目的とする旅行者数が最も多い地方は関東である
1 観光等を目的とする旅行者数が最も多い地方は沖縄である
2 地方ごとの旅行者数の合計に対する出張等の旅行者数の割合は、関東よりも東北の方が高い
3 地方ごとの旅行者数の合計に対する観光等の旅行者数の割合は、中部よりも近畿の方が高い
問2
次の文章を読み、空欄[オ][カ]に入れるのに最も適当なものを、後の解答群のうちから一つずつ選べ。ただし、解答の順序は問わない。
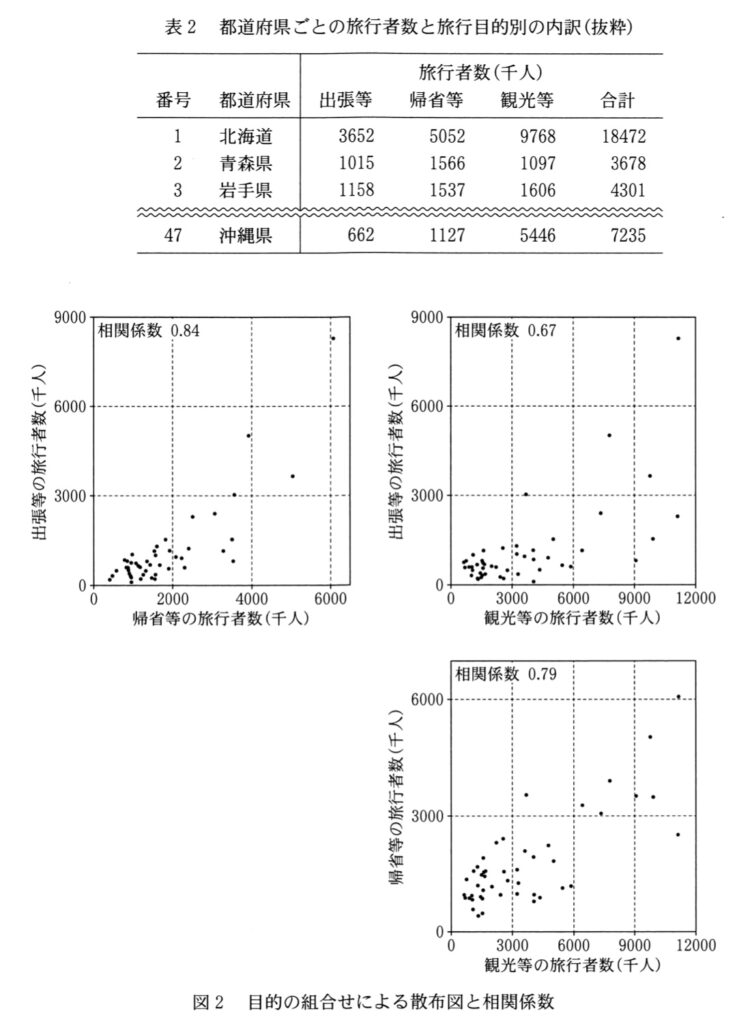
続いてUさんは、都道府県ごとの旅行者数と旅行目的別の内訳が集計されている表2をもとに、さらに詳細な分析を進めることにした。
Uさんはここで、目的別の旅行者数の間にどのような関係があるかについて関心をもった。そこでUさんは、図2のように、各目的の旅行者数を組み合わせた散布図を作成し、相関係数を求めた。
これらの散布図と相関係数のみから読み取れることは、[オ]ことや、[カ]ことなどである。
[オ] [カ]の解答群
0 二つの都道府県を比較して、観光等の旅行者数が多い方の都道府県は帰省等の旅行者数も必ず多い
1 すべての都道府県で、出張等の旅行者数は帰省等の旅行者数の1.5倍を下回る
2 それぞれの散布図で最も上に位置する都道府県は異なる
3 各都道府県について、ある目的の旅行者数が多くなるほど、他の目的の旅行者数も多くなる傾向にある
4 各都道府県で観光地をアピールすることで観光等の旅行者数を増やすことができれば、帰省等と出張等のいずれの旅行者数も増える
出典:独立行政法人 大学入試センター
尺度水準について
今回の共通テストでは、旅⾏・観光消費動向調査という身近なデータが使われていました。一見すると複雑に見えるデータですが、実は出題者は、私たちの「データを正しく見る力」があるかを試しているんです。
この問題に隠された意図を読み解くために、まずはデータを分類する4つのモノサシ(尺度水準)を理解しましょう。これらの知識があれば、グラフが何を伝えようとしているのか、一発で見抜けるようになります。
比例尺度と間隔尺度:ゼロの有無がモノを言う!
比例尺度と間隔尺度は、どちらも「等しい間隔」を持つデータですが、両者の違いは「絶対的なゼロ」があるかないかです。
- 比例尺度: 「絶対的なゼロ」が存在します。例えば、身長や体重です。身長0cmは「身長がない」状態を意味し、180cmは90cmのちょうど2倍と言えます。共通テストの問題で言えば、「旅行者数」がこれに当てはまります。旅行者数0人は「旅行者がいない」ことを意味するため、[イ]の回答は「0」になります。
- 間隔尺度: 「絶対的なゼロ」がありません。温度(摂氏・華氏)や西暦がこれにあたります。0℃は「温度がない」わけではなく「水の氷点」という特定の基準を表します。そして20℃は10℃の2倍の熱さとは言えません。
順序尺度と名義尺度:並べるか、分けるか?
次に、データに順序があるかないかで分類する2つのモノサシを見てみましょう。
- 順序尺度: データに「順序」はありますが、その間隔に意味がありません。例えば、テストの成績評価(優・良・可)や、大会の順位(1位・2位・3位)です。1位と2位の差が、2位と3位の差と同じとは限りませんね。
- 名義尺度: データに順序や大小関係は一切ありません。単に分類するための「名前」です。性別や血液型がこれにあたります。今回の問題では、「地方」がこれに該当します。「北海道」や「沖縄」に順序や優劣はありませんよね。そのため、[ア]の回答は「3」となります。
このように、グラフや表を読み解く前にそのデータがどの尺度で測られているのかを考えるだけで、問題の本質がグッと見えてきます。
棒グラフと帯グラフ
次に[ウ]と[エ]の答えを考えるため、棒グラフと帯グラフを確認する必要があります。なぜ、わざわざ2つのグラフが使われているのでしょうか?
出題者は、私たちがそれぞれのグラフが持つ「得意なこと」を理解しているか、そして「全体と部分の関係」を正確に読み取れるかを見ています。
- 棒グラフ: 個々の項目の「絶対的な量」や「大きさ」を比較するのに向いています。
- 帯グラフ: 全体を100%とした時の「内訳の割合」や「比率」を比較するのに向いています。
このグラフの特性を理解すれば、問題の選択肢を効率よく検証できます。
では、この知識を使って、[ウ]と[エ]の答えを導き出しましょう。
選択肢0:「帰省等を目的とする旅行者数が最も多い地方は関東である」
これは「個々の量」を比較する問題なので、棒グラフの出番です。(a)の棒グラフを見ると、関東の帰省等の旅行者数は約2万人と、他のどの地方よりも突出して多いことが一目瞭然です。これはグラフから直接読み取れる情報なので、この選択肢の内容は正しいです。
選択肢1:「観光等を目的とする旅行者数が最も多い地方は沖縄である」
これも「個々の量」を比較する問題なので、(a)の棒グラフを見ます。そうすると、関東の旅行者数が最多であることが分かるので、この選択肢の内容は誤りです。
選択肢2:「地方ごとの旅行者数の合計に対する出張等の旅行者数の割合は、関東よりも東北の方が高い」
これは「全体に対する部分の割合」を比較する問題なので、帯グラフを使います。(b)の帯グラフを見ると、東北の出張等の旅行者数を示す部分が、関東の部分よりも明らかに大きいことが分かります。これは帯グラフの得意分野であり、正しい内容です。
選択肢3「地方ごとの旅行者数の合計に対する観光等の旅行者数の割合は、中部よりも近畿の方が高い」
これも「全体に対する部分の割合」を比較する問題なので、(b)の帯グラフを見ます。そうすると、中部の観光等の割合が近畿よりも高いため、誤った内容であることが分かります。
このようにグラフが持つ特性を理解していれば、問題の意図を正確に読み取り、自信を持って正解を導き出すことができます。
散布図と相関係数
[オ] と[カ] の答えを考えるためには、3つの散布図を理解する必要があります。これらの散布図は、ただデータを並べているわけではありません。「2つのデータが、どのような関係にあるか?」を視覚的に訴えかけているのです。
- 散布図:2つの異なるデータの間にどのような関係があるかを点で表したグラフです。点が右肩上がりなら「一方が増えると、もう一方も増える」という関係(正の相関)が見て取れます。
- 相関係数:2つのデータがどれだけ同じように増えたり減ったりするかを表す数値で、-1から1の範囲を取ります。この数値が1に近ければ近いほど、強い正の相関があることを示します。
この2つを理解すれば、問題の選択肢に隠された意図を正確に読み解くことができます。
では、この知識を使って、[オ]と[カ]の答えを導き出しましょう。
選択肢0:「観光等の旅行者数が多い都道府県は帰省等の旅行者数も必ず多い」
この選択肢は、「観光等の旅行者数」と「帰省等の旅行者数」の間にどのような関係があるかを問うています。そこで散布図を見ると、観光等の旅行者数が多いのに帰省等の旅行者数が少ない都道府県も存在するため、この選択肢の内容は誤りだと分かります。
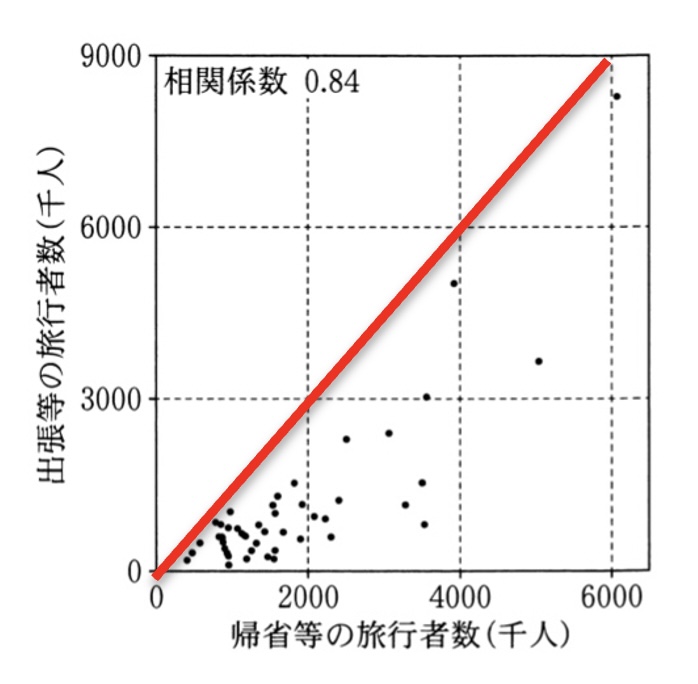
選択肢1:「すべての都道府県で、出張等の旅行者数は帰省等の旅行者数の1.5倍を下回る」
この選択肢の意図は、「散布図から傾きを読み取れるか」を問うことです。帰省等の旅行者数を横軸、出張等の旅行者数を縦軸とする散布図で、傾き1.5の直線を引いてみましょう。すると全ての点がこの直線の下に位置していることがわかります。これは、どの都道府県でも出張等の旅行者数が帰省等の1.5倍を下回っていることを意味するため、この選択肢の内容は正しいです。
選択肢2:「それぞれの散布図で最も上に位置する都道府県は異なる」
3つの散布図を詳細に確認すると、最も上にある点(出張等の旅行者数が最も多い点)が、すべてのグラフで同じ都道府県であることが分かります。したがって、この選択肢は誤った内容です。
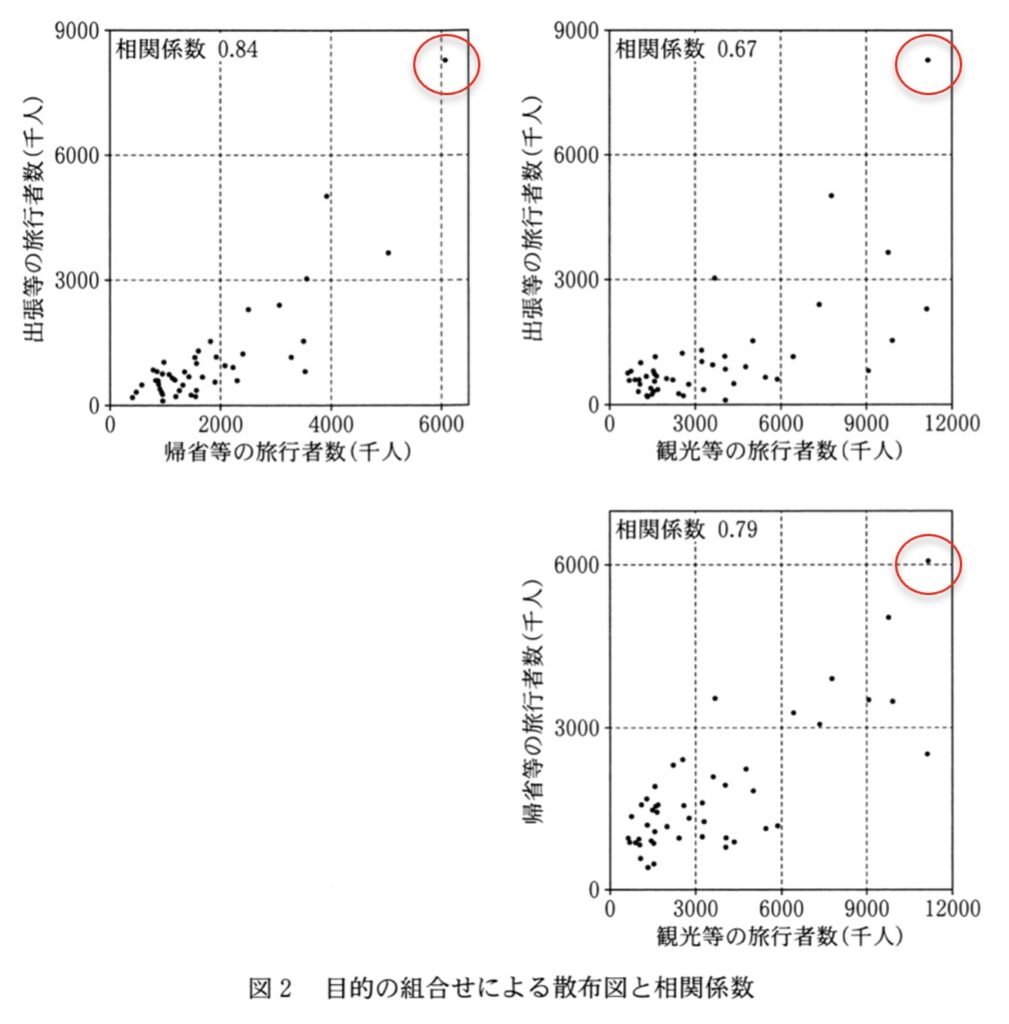
選択肢3:「各都道府県について、ある目的の旅行者数が多くなるほど、他の目的の旅行者数も多くなる傾向にある」
この選択肢は、「相関関係を読み取れるか」を問うものです。3つの散布図に示されている相関係数を見ると、それぞれ0.84、0.67、0.79と、すべて正の値であり、かつ1に近い数値です。これはどの組み合わせでも、一方が増えればもう一方も増える傾向が強いことを示しています。したがって、この選択肢の内容も正しいです。
選択肢4:「観光等の旅行者数が増えれば、帰省等と出張等のいずれの旅行者数も増える」
相関関係があることは分かりますが、因果関係があるとは断言できません。観光客を増やす施策が他の目的の旅行者数を増やす直接的な原因になるかは、このグラフからは判断できないため、誤った内容となります。
さいごに
ここまで読んで頂いた方は、データ分析の面白さをきっと感じて頂けたのではないでしょうか。次回の記事では、問3と問4で取り上げられていた内容について解説させていただければと思います。本日も最後までお読み頂き、誠にありがとうございました!次回の記事も楽しみにお待ち下さい。
タイムレスエデュケーションは、東京都文京区小石川、本駒込、新宿区下落合にて、プログラミング&ロボット教室を開校しております。当教室はお子さまが「誰にも奪われない強み」を見つけ、自分の意思で未来を選べるようになるための教室です。毎回の授業で「探究→創造→発信」を繰り返す構造化カリキュラムを通じて、「論理的思考力」「集中力」「表現力・創造力」「問題解決力」を育みます。秋の無料体験会も開催致しますので、ご興味のある方はぜひお申し込みください。心よりお待ちしております。
コースについて

