2025.10.21ブログ
【大学共通テスト 情報Ⅰ 解説】支払いとおつりのシミュレーション【文京区・新宿区】

こんにちは!文京区・新宿区にある小学生向けプログラミング教室のタイムレスエデュケーションです。今回は、大学入試共通テスト「情報Ⅰ」の大問2のBについて解説していきます。この問題は、「集金とおつり」という非常に身近なテーマを通して、コンピュータを使った未来予測の技術「シミュレーション」の考え方を学べる、非常によくできた問題です。「シミュレーション」と聞くと難しそうですが、その考え方の基本は、実はとてもシンプル。この記事を読めば、その本質から問題の解き方まで、きっと深く理解できるはずです。それでは、一緒に見ていきましょう!
これまでの共通テスト解説記事は下記のリンクからご覧ください!
第問4(part1)
はじめに:シミュレーションとは
そもそも、シミュレーションとは何でしょうか。情報Ⅰの教科書では、シミュレーションを次のように説明しています。
シミュレーションとは、現象の予測をするために、モデルにいろいろな変更を加え試してみることを意味する。(黒上晴夫ほか編「情報Ⅰ」日本文教出版 p150)
モデルとは、「あらわしたいものの本質的な部分を強調し、それ以外の要素や条件を省略するなどして単純化したもの」です。つまり、現実の世界で起こる様々な現象や問題をモデルにして、コンピュータの中で再現しその動きを試すことで解決方法を探る、ということです。実際に実験することが難しいこと、例えば費用がかかりすぎてしまうことや実験に危険が伴うものなどを、コンピュータ上で安全かつ低コストで実験することができます。
手順としては、最初に、問題をモデル化し、その後シミュレーションを行い、その結果を分析することで問題を解決していきます。今回は問題を読み解きながら、シミュレーションとして何をしているのか確認していきたいと思います。
試験問題を確認
大問2 B 次の文章を読み、後の問い(問1〜3)に答えよ。
Mさんは、あるグループの会計係をしており10人のメンバーから一人6000円ずつ集めることになった。Mさんは、以前集金をしたときにおつりに困ったことがあったので、メンバー全員におつりを渡すための千円札を何枚用意しておくのがよいか、次の条件でシミュレーションすることにした。
・グループのメンバーは、来た順番に一人ずつMさんにお金を支払う。
・メンバーは必ず千円札6枚(6000円)または一万円札(10000円)のいずれかでMさんに支払う。
・メンバーが一万円札で支払った場合、おつりの4000円は千円札4枚で渡す。
・メンバーが千円札6枚で支払う確率を30%、一万円札で支払う確率を70%と考える。
シミュレーションは表計算ソフトウェアで1以上10以下の整数が同じ確率で出現する乱数rを用い、次のように考えて行った。
rが3以下の場合:千円札6枚で支払う
rが4以上の場合:一万円札1枚で支払う
問1 次の文章を読み、空欄コ〜セに当てはまる数字をマークせよ。
Mさんの手元の千円札の枚数を最初0枚として、シミュレーションした結果、表1のようになった。
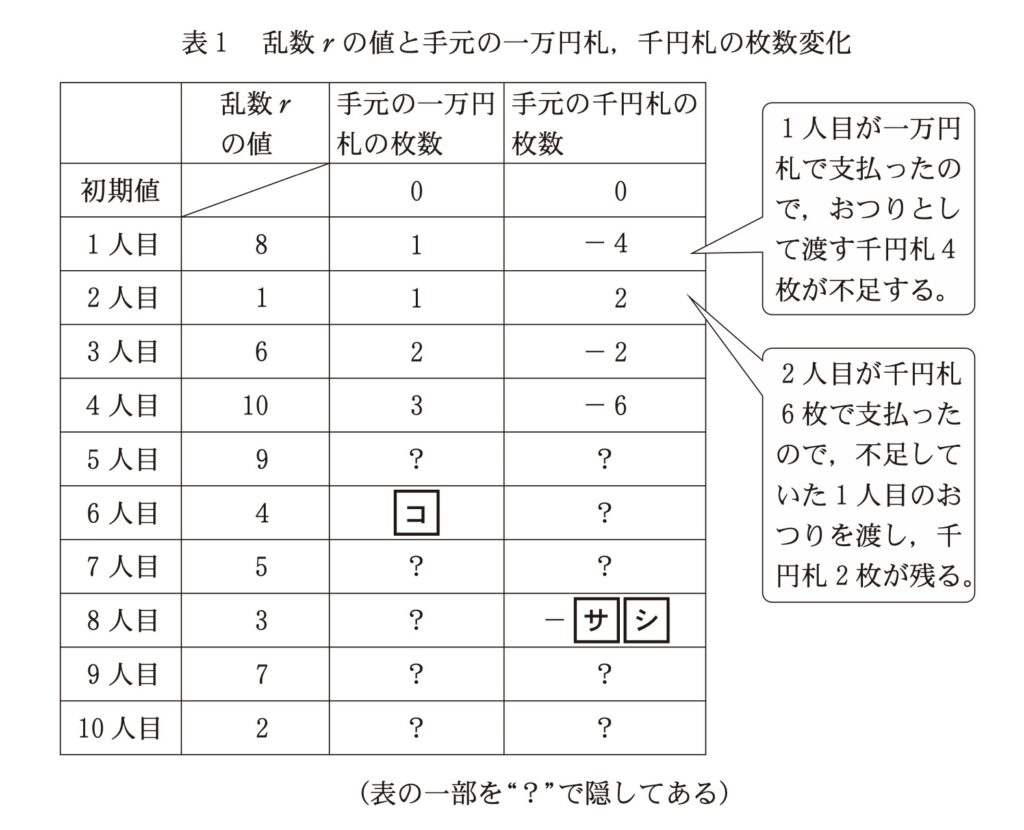
なお、この表の「手元の千円札の枚数」が負の数の場合、Mさんが渡さなければならないおつりの千円札が、その数の絶対値の枚数分不足していることを意味する。そこでMさんは、「手元の千円札の枚数」の最小値を調べ、その絶対値の枚数の千円札を事前に準備しておけば、おつりに困らないと考えた。この考えによると、今回行った1回のシミュレーションの場合、千円札(ス)(セ)枚を事前に準備しておけば、一度も千円札が不足することなく集金できることになる。
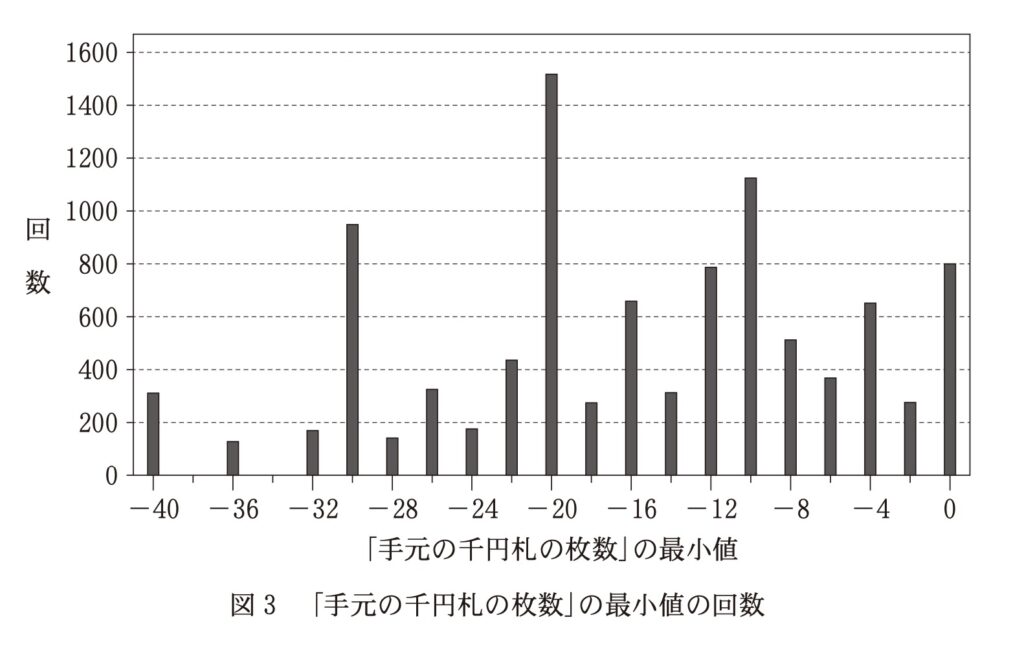
問2 Mさんは、1回のシミュレーション結果では判断できないと考え、このシミュレーションを10000回行った。図3は各シミュレーションでの「手元の千円札の枚数」の最小値を横軸に、その回数を縦軸に表したものである。この結果に関する考察して最も適当なものを、次の0〜3のうちから一つ選べ。(ソ)
0 全員が一万札で支払うケースはなかった。
1 最後まで千円札が不足しなかったのは、全回数の1割以下である。
2 別の乱数を使って10000回シミュレーションを行っても、最終的な結果のグラフはまったく同じになる
3 全員が千円札でお金を支払ったケースが1回以上ある。
問3 次にMさんは、事前に千円札を20枚用意した場合について考えた。この場合、メンバー10人から順に集金した際に起こることがないケースを、次の0〜3のうちから1つ選べ。(タ)
0 最初の1人が千円札で支払ったとしても、途中でおつりの千円札が不足するケース。
1 用意した千円札を全く使うことなく全員からの集金を終えるケース。
2 千円札で支払った人が5人いて、途中でおつりの千円札が不足するケース
3 一万円で支払った人が8人いて、途中でおつりの千円札が不足せず全員から集金を終えるケース。
モデル化とシミュレーション
この問題文は、シミュレーションの手順に沿って話が進んでいます。1つずつ確認していきたいと思います。
モデル化
シミュレーションをする前に、問題をモデル化する必要があります。モデル化は以下の手順で行われます。
1. モデル化の目的を明確にする
2. モデルを構成する要素とその関係を明らかにする
3. モデルを数式や図に表す
1つ目のモデル化の目的については、この問題は「Mさんは、以前集金をしたときにおつりに困ったことがあったので、メンバー全員におつりを渡すための千円札を何枚用意しておくのがよいか」とある通り、「おつりに困らない最適な千円札の枚数を知ること」がモデル化の目的となっています。
手順の2番目は、現実の現象を単純化して、ルールを決める段階です。問題文にはシミュレーションの条件について以下のように書かれていました。
1. グループのメンバーは、来た順番に一人ずつMさんにお金を支払う。
2. メンバーは必ず千円札6枚(6000円)または一万円札(10000円)のいずれかでMさんに支払う。
3. メンバーが一万円札で支払った場合、おつりの4000円は千円札4枚で渡す。
4. メンバーが千円札6枚で支払う確率を30%、一万円札で支払う確率を70%と考える。
支払い方法やお金の流れ、行動の確率といった、モデルを構成する要素とその関係性を具体的に決めています。
その後、手順2で決めたルールをコンピュータで扱うことができるようにしているのが手順3です。問題文にある、「シミュレーションは表計算ソフトウェアで1以上10以下の整数が同じ確率で出現する乱数rを用い、次のように考えて行った。rが3以下の場合:千円札6枚で支払う rが4以上の場合:一万円札1枚で支払う」が該当します。これで、コンピュータで計算できるよう条件式に置き換えることができました。これにより、コンピュータ上でシミュレーションをする準備が整ったことになります。
モンテカルロ法
今回の「集金する時にどの支払い方法を選ぶか」という事象は、どうなるか分からない「確率的な変動」を含んでいます。このように、確率が絡む事象をシミュレーションをする代表的な手法が「モンテカルロ法」です。この手法の土台になっているのが、「大数の法則」です。これは、「標本のサイズ(=シミュレーションの試行回数)を大きくしていくと、その標本平均が理想的な状態(=母集団の平均)に近づいていく」という法則です。モンテカルロ法はこの法則を利用し、乱数を使ってシミュレーションを何万回も繰り返すことで、その膨大な結果の平均を求めます。つまり、試行回数を重ねる(標本のサイズを大きくする)ほど、その平均値は統計的に安定していきます。そして、その結果は理想的な状態(=母集団の平均)」、つまり「本当に知りたい答え」にに近い値を推定することができます。こうすることで、シミュレーション結果はより信頼性の高いものになります。
シミュレーションの手順
ここからは、モデルを基にシミュレーションしていく段階です。シミュレーションの手順は、以下の通りになっています。
1. モデルを使ってシミュレーションする
2. シミュレーションの結果を実際の現象と比較し、仮説やモデルを修正する
3. シミュレーションの結果を用いて問題を解決する
最初に、モデルを使って実際に計算し、その結果を分析して問題を解決するという流れになっています。この流れは、問1から3まで順番に解くことで追体験できるようになっています。では、ここからは、問1から順番に確認していきましょう。
問題解説
問1:モデルを使ったシミュレーション
この問題は、モデル化で定義したルールに基づき、実際に10人分の集金を1回シミュレーションした結果である表1の空欄を埋めるものです。支払いのルールは、モデル化で定義したルール通り、乱数rの値に応じて、千円札が「+6枚」されるか「-4枚」される、というものです。
計算の過程
まずは、表に示されたMさんの状況を追いかけて、空欄を埋めていきましょう。
・【コ】6人目までの一万円札の枚数:表1の乱数を見ると、6人目までで乱数が「4以上」だったのは、1,3,4,5,6人目の5人です。したがって、一万円札で支払ったのは5人。空欄コは5です。
・【サ・シ】8人目を終えた時点の千円札の枚数:手元の千円札が0枚からどう変化したか、一人ずつ見ていきましょう。
・6人目まで:一万円札が5回(-4枚 × 5人 = −20枚)、千円札が1回(+6枚 × 1人 = +6枚)です。計算すると、手元の千円札は、-20 + 6 = -14枚です。
・7人目:乱数が「8」なので一万円で支払い。手元の千円札はさらに4枚減り、-14 -4 = -18枚となります。
・8人目:乱数が「1」なので千円札で支払い。手元の千円札は6枚増えるので、-18 + 6 = -12枚となります。
よって、8人目を終えた時点で千円札は12枚不足している状態です。空欄サは1、空欄シは2が正解です。
準備すべき千円札の枚数(リスク管理)
このシミュレーションの目的は、「おつりに困らないように、事前に何枚千円札を用意すべきか?」、つまり最悪の事態を想定することです。シミュレーション全体で、手元の千円札が最も少なくなった(マイナスの値が最も大きくなった)瞬間を探します。先ほどの計算の続きを行い、表を埋めていきましょう。
・9人目:乱数が「5」なので一万円で支払い。手元の千円札は4枚減り、-12 -4 = -16枚になります。
・10人目:乱数が「2」なので千円札で支払い。手元の千円札は6枚増え、-16 + 6 = -10枚
全10人を通して、最も千円札が不足したのは、7人目を終えた時点の「−18枚」でした。したがって、この最悪の事態に備えるためには、事前に18枚の千円札があれば安心です。よって、空欄スには1、空欄セには8が当てはまります。
問2:10000回のシミュレーション結果を読み解く
シミュレーションの次の段階は、シミュレーションの結果の傾向を分析、評価して仮説やモデルを修正します。ただし、1回だけのシミュレーションでは、偶然かもしれないため、何度もシミュレーションを繰り返します。この問題でも、Mさんは同じシミュレーションを10000回行っています。その結果を図3のグラフにして傾向を分析するのが、この問題です。このデータから何が言えるか、選択肢を一つずつ吟味していきましょう。
【選択肢0】「全員が一万円札で支払うケース」は、おつりで千円札が-4枚 × 10人 = -40枚にななるはずです。グラフをの左端を見ると、最小値が「−40」の棒グラフが確かに存在します。つまり、このケースは実際にあったことなので、この選択肢は間違いです。
【選択肢1】「最後まで千円札が不足しなかったケース」とは、シミュレーション中の千円札の枚数の最小値が「0以上」であったということです。グラフで最小値が「0」の回数は約800回。全10000回の1割は1000回なので、800回は一割以下ですね。したがって、この選択肢は正しいです。
【選択肢2】シミュレーションは「乱数」という偶然に基づいているため、もう一度10000回やり直しても、結果は完全に同じにはなりません。グラフの形は似るかもしれませんが、全く同じになる保証はないため、この選択肢は間違いです。
【選択肢3】「全員が千円札で支払うケース」は、手元の千円札は増え続けるので最小値は「0」になります。しかし、グラフの「最小値0」には、途中で一万円札の支払いがあっても結果的に一度もマイナスにならなかったケースも含まれています。このグラフだけでは「全員が千円札で支払ったケースが1回以上あったとは断定できないため、この選択肢は間違いです。
以上から、最も適当な選択肢は1となります。
問3:問題解決に向けて
最後の問題は、シミュレーションの最終段階である、分析結果を基に結論を導き出す段階です。問2で実施した10000回のシミュレーション結果の考察を踏まえて、「事前に千円札を20枚用意した」場合はどうなるかという問題解決のための検討を行います。選択肢の中から「絶対に起こらないケース」はどれかを探しましょう。
【選択肢0】最初の1人が千円札で支払うと、手元の千円札は20 + 6 = 26枚。残りの9人全員が一万円札で支払うと、必要なおつりは4 × 9 = 36枚。これでは、26 - 36 = -10枚となり、不足する可能性があります。
【選択肢1】全員が千円札で支払えば、用意した千円札は使われず、枚数は増え続けます。これは起こり得ます。
【選択肢2】千円札での支払いが5人(6枚 × 5人 = 30枚)、一万円札での支払いが5人(-4枚 × 5人 = -20枚)ケースを考えます。おつりが最も厳しくなるのは、最初に5人連続で一万円札で支払われた場合です。このとき、手元の千円札は0枚となります。ぴったり0枚にはなりますが、不足していません。したがって、「途中でおつりの千円札が不足するケース」は絶対に起こりません。
【選択肢3】一万円札での支払い人が8人(-4枚 × 8人 = -32枚)、千円札での支払いが2人(6枚 × 2人 = 12枚)のケースでは、最終的な千円札の枚数は、20 + 12 -32 = 0枚です。例えば、最初に2人が千円札で支払えば手元の千円札は32枚になり、その後の8人のおつりを不足なく支払うことができます。これは、起こり得ることです。
したがって、起こることがないケースは2となります。
まとめ
今回の解説はいかがでしたでしょうか。この問題は、一連の流れがシミュレーションの流れと同じであり、問題を解きながらシミュレーションの体験ができるものでした。シミュレーションがどういった手順で行われているのかを理解することができたと思います。また、問題を解く際は特別な知識は必要なく、問題やグラフを丁寧に読み解くことが大切でした。情報Ⅰの知識ももちろん大切ですが、読解力を鍛えることも重要だと言えます。
プログラミング教室をお探しなら「タイムレスエデュケーション」
タイムレスエデュケーションは文京区茗荷谷、本駒込、新宿区下落合にて、プログラミング&ロボット教室を開校しております。開講しているコースの詳細は下記の「コースについて」からご確認ください。また、無料体験会も随時実施しております。ご興味のある方はお気軽にお問い合わせください。心よりお待ちしております。

